Ersättning av grad n. Exponentiering: regler, exempel. Exponentieringskoncept

Mål:överväga begreppet substitution, identisk substitution,

förklara hur operationerna för att multiplicera substitutioner, hitta inversa substitutioner utförs,

lista egenskaperna hos substitutionsprodukten,

överväga begreppen inversion, jämnt utbyten

visa hur substitutioner tillämpas i kryptografi

En gång fick Thomas ett telegram från en av sina vänner. Detta telegram var konstigt. Här är vad som skrevs i den: "yazzeirponchors medzh".

Kan du "läsa" den här texten? Efter en liten tanke förstod Thomas hemligheten med detta telegram. Han blev inbjuden att besöka. Han bestämde sig för att svara i samma anda. Jag komponerade ett svarstelegram och krypterade det på samma sätt. Resultatet är ett register med två rader:

"Jag kommer träffa dig på lördag",

"" etyachertswutobbuswudeirp "".

Efter krypteringens slut ville Thomas utföra all sin korrespondens med en vän endast i krypterade texter, och bytte då och då metoden för kryptering. Därför började han ivrigt utveckla en krypteringsmetod.

Han bestämde sig för att ersätta bokstäverna i originaltexten med de positionssiffror som dessa bokstäver upptar. Här är listan över nummer som Foma fick för sin väns telegram:

(1, 2, 3, ... , 18).

Sedan märkte han att krypteringstexten skiljer sig från originalet endast i bokens ändrade ordning. Hur brevordern ändras är lätt att se med samma positionssiffror. Till exempel kan chiffertexten i ett telegram från en vän Thomas nu presenteras i form av en lista:

(18, 17, 16, . . . , 3, 2, 1).

Att jämföra de två listorna ger en ledtråd för att kryptera texten:

.

Den symboliska posten lyder så här: "1 går till 18". En annan notation används ofta istället :.

Pilarnas riktning bestämmer ordningen kryptering text. Till exempel bör en bokstav i den första positionen i krypteringstexten inta den 18: e positionen i krypteringstexten.

Om pilarnas riktning ändras till motsatsen, bestämmer samma tvåradstabell ordningen transkriptioner text. Till exempel bör en bokstav i den 18: e positionen i krypteringstexten inta den första positionen i den dekrypterade texten.

Slutligen, om den första raden alltid är associerad med källtexten, finns det inget behov av att använda pilar. (När den är krypterad är originaltexten den krypterade texten, och när den krypteras är den krypterad).

Thomas insåg allt detta och skrev snabbt ner nyckeln till den andra krypteringen av sitt telegram:

Det återstår bara att kommunicera den här nyckeln till din vän på något sätt, och sekretessen för korrespondensen är garanterad!

Om du förstår Thomas idéer, här är hans krypterade favoritordstäv:

"vattenkoka".

Det är krypterat med nyckeln:

Krypteringsnyckel:

"Lita på men kolla!"

Du har antagligen redan gissat att många krypteringsnycklar av detta slag kan uppfinnas. Var och en av dem kan representeras som en tvåradig tabell:

.

Här innehåller den översta raden alla naturliga tal från 1 till NS i stigande ordning. Nedre raden erhålls genom viss permutation av siffror från den översta raden. Hela bordet som helhet kallas orderbyte NS.

Tänk på uppsättningen , där varje element presenteras endast en gång. Då kallas en en-till-en-mappning av en uppsättning på sig själv utbyte grad NS.

Massor av byten NS-th grad anges.

Förhållandet är binärt, därför är substitutioner vanligtvis skrivna i form av en tvåradig matris, i vilken den första raden förbilderna skrivs, och i den andra - deras bilder:

Om förbilderna (argumenten) är ordnade i stigande ordning (kallas en sådan substitutionspost kanonisk... Om argumenten inte är skrivna i stigande ordning kan du genom att ändra ordning på kolumnerna (i det här fallet ändras inte själva substitutionen, men endast matchningens uttalningsordning), den översta raden till en ordnad form:

När det är möjligt kommer vi att använda den kanoniska notationen. En sådan inspelning påträffades när vi spelade in en permutation från NS element. Observera att förbilden av permutationen är en godtycklig ändlig uppsättning, och preimagen av permutationen är obligatorisk.

Låt oss hitta antalet möjliga olika utbyten av examen NS... Eftersom varje kanonisk permutation är ekvivalent med motsvarande permutation, är antalet permutationer NS-th grad är lika med antalet permutationer från NS element, det vill säga uppsättningen består av element.

Låt oss gå tillbaka till Thomas. Använda nyckelbyte

han krypterade ett ett-meddelande och skickade det till en vän. Han krypterade det okrypterade meddelandet igen, men med en annan nyckel.

Det resulterande dubbelkrypterade meddelandet han riktade till dig: "snoas".

Kryptera detta meddelande. , " Tall»

Du kan göra dekrypteringsprocessen mycket snabbare om du vet hur en algebraisk operation utförs på substitutioner. Denna operation kallas multiplikation av substitutioner.(Om du vill kan du kalla det annorlunda, för det har ingenting att göra med den vanliga multipliceringen av siffror).

Låt oss titta på ett exempel på hur det utförs. Låt oss multiplicera substitutionerna med hjälp av vilket Fomas meddelande krypterades:

Multiplikationsförfarandet reduceras till sekventiella substitutioner.

I det första bytet ( MEN): 1 → 5;

i det andra bytet (I): 5 → 1;

Som ett resultat får vi: 1 → 1.

På samma sätt följer "2 → 2" och "2 → 3": "2 → 3". Genom att utföra ytterligare tre argument av denna typ får vi produktsubstitutionen

Använda bytet AB som en scrambler kan du nu kryptera Thomas "snoas" -meddelande på en gång. Samtidigt kommer du att kontrollera dig själv. ( VA= « pump»)

Om du är intresserad kan du komma med dina egna meddelandehanterare och hålla hemlig korrespondens med vänner.

Dechiffrera meddelanden, du blev bekant med den algebraiska operationen på nya substitutionsobjekt. Om några av er inte bara är intresserade av krypteringen utan också av själva utbytena kan man lära känna dem bättre genom att utföra följande uppgifter.

ÖVNING 1... Hitta ersättningsprodukterna:

UPPGIFT 2. Hitta en bit VA utbyten MEN och I, som diskuterats ovan. Använda bytet VA som en scrambler, dechiffrera meddelandet "cod" igen. Jämför resultatet med resultatet av den tidigare dekrypteringen. Då kan du se om permutationsmultiplikationen är kommutativ.

Låt det ges två byten och dessutom

Vi fick reda på vad graden av ett tal är i allmänhet. Nu måste vi förstå hur man korrekt beräknar det, dvs. höja siffrorna till en makt. I detta material kommer vi att analysera de grundläggande reglerna för beräkning av graden i fallet med en hel, naturlig, fraktionerad, rationell och irrationell exponent. Alla definitioner kommer att illustreras med exempel.

Exponentieringskoncept

Låt oss börja med att formulera grundläggande definitioner.

Definition 1

Exponentiering- detta är beräkningen av värdet på ett tal.

Det vill säga orden "beräkna värdet av en makt" och "höja till en makt" betyder samma sak. Så om problemet är "Höj siffran 0, 5 till den femte effekten", bör det förstås som "beräkna effektens värde (0, 5) 5.

Nu kommer vi att ge de grundläggande regler som måste följas i sådana beräkningar.

Låt oss komma ihåg vilken grad ett tal har med en naturlig exponent. För en effekt med bas a och exponent n kommer detta att vara produkten av n-antal faktorer, var och en är lika med a. Det kan skrivas så här:

För att beräkna effektens värde måste du utföra multiplikationsåtgärden, det vill säga multiplicera effektbaserna ett visst antal gånger. Själva konceptet med en examen med en naturlig indikator bygger på förmågan att snabbt multiplicera. Här är några exempel.

Exempel 1

Villkor: höja - 2 till kraften 4.

Lösning

Med hjälp av definitionen ovan skriver vi: (- 2) 4 = (- 2) · (- 2) · (- 2) · (- 2). Därefter behöver vi bara följa de angivna stegen och få 16.

Låt oss ta ett mer komplicerat exempel.

Exempel 2

Beräkna värdet 3 2 7 2

Lösning

Denna post kan skrivas om som 3 2 7 · 3 2 7. Tidigare tittade vi på hur man korrekt multiplicerar de blandade siffrorna som nämns i tillståndet.

Låt oss utföra dessa åtgärder och få svaret: 3 2 7 3 2 7 = 23 7 23 7 = 529 49 = 10 39 49

Om problemet indikerar behovet av att höja irrationella tal till en naturlig kraft, måste vi först runda deras baser till en siffra som gör det möjligt för oss att få svar på erforderlig noggrannhet. Låt oss titta på ett exempel.

Exempel 3

Fyrkantig π.

Lösning

Låt oss först runda den till närmaste hundradel. Sedan π 2 ≈ (3, 14) 2 = 9, 8596. Om π ≈ 3. 14159, då får vi ett mer exakt resultat: π 2 ≈ (3, 14159) 2 = 9, 8695877281.

Observera att behovet av att beräkna graderna av irrationella tal i praktiken uppstår relativt sällan. Vi kan sedan skriva svaret i form av själva kraften (ln 6) 3 eller transformera, om möjligt: ​​5 7 = 125 5.

Separat bör det anges vilken första grad av ett nummer är. Här kan du helt enkelt komma ihåg att valfritt nummer som höjs till den första makten kommer att förbli av sig själv:

Detta framgår tydligt av posten. .

Det beror inte på graden av examen.

Exempel 4

Så, (- 9) 1 = - 9 och 7 3, höjd till första kraften, kommer att förbli lika med 7 3.

För enkelhets skull analyserar vi tre fall separat: om exponenten är ett positivt heltal, om det är noll och om det är ett negativt heltal.

I det första fallet är detta detsamma som att höja till en naturlig kraft: trots allt tillhör positiva heltal uppsättningen naturliga tal. Vi har redan beskrivit hur man arbetar med sådana grader ovan.

Låt oss nu se hur man korrekt höjer till nolleffekten. Med en annan radix än noll ger denna beräkning alltid 1. Vi har redan förklarat tidigare att den 0: e effekten av a kan definieras för alla reella tal som inte är lika med 0 och en 0 = 1.

Exempel 5

5 0 = 1 , (- 2 , 56) 0 = 1 2 3 0 = 1

0 0 - ej definierad.

Vi har bara ett fall av en grad med en helt negativ exponent. Vi har redan diskuterat att sådana grader kan skrivas som en fraktion 1 a z, där a är valfritt tal, och z är ett heltal negativ exponent. Vi ser att nämnaren för denna fraktion inte är något annat än en vanlig makt med en helt positiv exponent, och vi har redan lärt oss hur man beräknar den. Låt oss ge exempel på uppgifter.

Exempel 6

Lyft 2 till makten - 3.

Lösning

Med hjälp av definitionen ovan skriver vi: 2 - 3 = 1 2 3

Låt oss beräkna nämnaren för denna fraktion och få 8: 2 3 = 2 · 2 · 2 = 8.

Då är svaret: 2 - 3 = 1 2 3 = 1 8

Exempel 7

Lyft 1, 43 till makten - 2.

Lösning

Låt oss omformulera: 1, 43 - 2 = 1 (1, 43) 2

Vi beräknar kvadraten i nämnaren: 1.43 · 1.43. Decimalfraktioner kan multipliceras på detta sätt: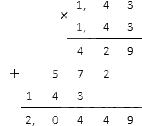

Som ett resultat fick vi (1, 43) - 2 = 1 (1, 43) 2 = 1 2, 0449. Det återstår för oss att skriva detta resultat i form av en vanlig fraktion, för vilken det är nödvändigt att multiplicera det med 10 tusen (se materialet om konvertering av fraktioner).

Svar: (1, 43) - 2 = 10000 20449

Ett separat fall höjer ett tal till minus första effekten. Värdet på denna grad är lika med det inversa av det ursprungliga basvärdet: a - 1 = 1 a 1 = 1 a.

Exempel 8

Exempel: 3 - 1 = 1/3

9 13 - 1 = 13 9 6 4 - 1 = 1 6 4 .

Hur man höjer ett tal till en bråkdel

För att utföra en sådan operation måste vi komma ihåg den grundläggande definitionen av en grad med en fraktionerad exponent: a m n = a m n för alla positiva a, heltal m och naturliga n.

Definition 2

Således måste beräkningen av bråkstyrkan utföras i två steg: att höja till ett heltal och hitta roten till den n: te kraften.

Vi har likheten a m n = a m n, som, med tanke på rötternas egenskaper, vanligtvis används för att lösa problem i form a m n = a n m. Det betyder att om vi höjer talet a till en bråkdel av m / n, så extraherar vi först den n: te roten till a, sedan höjer vi resultatet till en effekt med ett heltalsexponent m.

Låt oss illustrera med ett exempel.

Exempel 9

Beräkna 8 - 2 3.

Lösning

Metod 1. Enligt den grundläggande definitionen kan vi representera den som: 8 - 2 3 = 8 - 2 3

Låt oss nu beräkna graden under roten och extrahera den tredje roten från resultatet: 8 - 2 3 = 1 64 3 = 1 3 3 64 3 = 1 3 3 4 3 3 = 1 4

Metod 2. Vi omvandlar grundlikheten: 8 - 2 3 = 8 - 2 3 = 8 3 - 2

Därefter extraherar du roten 8 3 - 2 = 2 3 3 - 2 = 2 - 2 och kvadrerar resultatet: 2 - 2 = 1 2 2 = 1 4

Vi ser att lösningarna är identiska. Du kan använda den på vilket sätt du vill.

Det finns tillfällen då graden har en exponent uttryckt som ett blandat tal eller decimalfraktion. För att göra beräkningarna enklare är det bättre att ersätta den med en vanlig bråkdel och räkna den enligt ovan.

Exempel 10

Höj 44,89 till 2,5.

Lösning

Vi konverterar indikatorns värde till en vanlig bråkdel: 44, 89 2, 5 = 44, 89 5 2.

Och nu utför vi i ordning alla ovan nämnda åtgärder: 44, 89 5 2 = 44, 89 5 = 44, 89 5 = 4489100 5 = 4489100 5 = 67 2 10 2 5 = 67 10 5 = = 1350 125 107 100 000 = 13 501, 25107

Svar: 13501, 25107.

Om det finns stora siffror i täljaren och nämnaren för en fraktionerad exponent, är det ganska svårt att beräkna sådana grader med rationella exponenter. Det kräver vanligtvis databehandling.

Låt oss dröja separat på graden med nollbas och fraktionerad exponent. Ett uttryck av formen 0 m n kan ges följande betydelse: om m n> 0, då 0 m n = 0 m n = 0; om m n< 0 нуль остается не определен. Таким образом, возведение нуля в дробную положительную степень приводит к нулю: 0 7 12 = 0 , 0 3 2 5 = 0 , 0 0 , 024 = 0 , а в целую отрицательную - значения не имеет: 0 - 4 3 .

Hur man lyfter ett tal till en irrationell makt

Behovet av att beräkna värdet på graden, i vilken exponent det finns ett irrationellt tal, uppstår inte så ofta. I praktiken är uppgiften vanligtvis begränsad till att beräkna ett ungefärligt värde (upp till ett visst antal decimaler). Detta beräknas vanligtvis på en dator på grund av komplexiteten i sådana beräkningar, så vi kommer inte att dröja vid detta i detalj, vi kommer bara att ange de viktigaste bestämmelserna.

Om vi ​​behöver beräkna värdet på exponenten a med en irrationell exponent a, tar vi den decimala approximationen av exponenten och beräknar den. Resultatet blir ett ungefärligt svar. Ju mer exakt den decimala approximationen, desto mer exakt är svaret. Låt oss visa med ett exempel:

Exempel 11

Beräkna det ungefärliga värdet 2 till 1.174367 effekt ....

Lösning

Vi begränsar oss till decimala approximationen a n = 1, 17. Låt oss göra beräkningar med detta nummer: 2 1, 17 ≈ 2, 250116. Om vi ​​till exempel tar approximationen a n = 1, 1743, blir svaret lite mer exakt: 2 1, 174367. ... ... ≈ 2 1, 1743 ≈ 2, 256833.

Om du märker ett fel i texten markerar du det och trycker på Ctrl + Enter

Definition 5. Utbyte N: e graden en en-till-en-mappning av uppsättningen på sig själv kallas. Ersättning skrivs vanligtvis med två N-permutationer skrivna under varandra:

, (1)

Var genom betecknar det nummer som elementet går in i när det ersätts i, dvs .; i = 1,2, ..., N.

I en sökningspost kan du byta kolumner på något sätt. Till exempel är alla tre av följande substitutioner lika.

. (2)

I synnerhet varje ersättning N-te examen kan skrivas som:

.

Med denna form av notering skiljer sig olika substitutioner bara genom permutationerna i botten. Sedan, i kraft av sats 1, fick vi följande uttalande.

Sats 4.Antalet olika substitutioner för den n: e graden är N.

Definition 6.Enligt antalet inversioner i bytetär summan av antalet inversioner i den första och andra substitutionsraden.

Vi betecknar antalet inversioner i ersättningen med symbolen. Ersättningen kallas Även, om numret är jämnt och det kallas Udda om antalet är udda. Ett jokertecken är ett tal:

.

Därför är jokertecken 1 eller -1, beroende på om bytet är jämnt eller udda.

Med stöd av sats 2, när kolumnerna i substitutionen är permuterade, omvandlas pariteten för permutationerna i den nedre och övre raden av substitutionen samtidigt. Följaktligen bevaras permutationens paritet. Från detta och Theorem 3 får vi följande substitutionsegenskaper.

1. Paritet och jokertecken är oberoende av jokerteckenets form.

2. När N> 1 antal jämna byten N-th grad är lika med antalet udda byten och är lika med.

Exempel 4 Substitution (2) är udda och har ett -1-tecken, även om det för olika notationsformer har 3, 7, 5 inversioner.

Låt oss visa att uppsättningen av alla permutationer N-th-graden bildar en grupp med avseende på funktionen för multiplikation av substitutioner, definierade nedan. Denna grupp är av stor betydelse i algebra, kallad Symmetrisk Gruppen och betecknas med symbolen.

Definition 7. Genom produkten av substitutioner och N-th grad är sammansättningen av dessa uttalanden som mappningar, det vill säga för alla vi har. Vi betecknar

Eftersom sammansättningen av två bijektiva kartläggningar är en bijektiv kartläggning, då produkten av två permutationer N-te grad det finns underlägg N-te grad. I praktisk multiplikation av substitutioner utförs den högra substitutionen först och sedan den vänstra. Till exempel,

Sats 5.Uppsättningen av alla permutationer av den n: e graden bildar en grupp med avseende på funktionen för multiplicering av permutationer.

Bevis. Mot bakgrund av ovanstående är operationen för multiplikation av substitutioner en binär algebraisk operation. Låt oss kontrollera gruppens axiom.

Substitutionsmultiplikation är associerande. Ja, låt det vara. Sedan för alla

Definition ... Varje en-till-en-mappning av uppsättningen A av de första n naturliga siffrorna på sig själv kallas utbyten-te grad, och uppenbarligen, vilken permutation som helst A kan skrivas med två permutationer undertecknade varandra

Genom α i betecknar här numret i vilket substitutionen A omvandlar talet i , i = 1, 2, …, n.

Låt oss skriva en under de andra två permutationerna av n tecken, med de resulterande två raderna inom parentes; till exempel n = 5:

Vi kommer att säga att antalet är 3 går över i nummer 5, nummer 5 går i 2, nummer 1 går i 3, nummer 4 går i 4 (eller förblir på plats) och slutligen går nummer 2 i 1. Således, två permutationer, skrivna under varandra i form ( 2) definiera några en-till-en-kartläggning uppsättningar av de fem första naturliga siffrorna på sig själv, det vill säga en kartläggning som tilldelar vart och ett av de naturliga numren 1, 2, 3, 4, 5 ett av samma naturliga nummer och olika nummer tilldelas olika nummer.

Det är uppenbart att en-till-en-mappningen av uppsättningen av de fem första naturliga siffrorna, som vi fick med hjälp av (2), kunde erhållas genom att skriva en under varandra och några andra par av permutationer med fem symboler. Dessa register erhålls från (2) genom flera transpositioner (permutationer) av kolumner; sådana är till exempel

I alla dessa poster går 3 till 5, 5 till 2 och så vidare.

Substitution A har många olika poster i formuläret (1). Så, (2) och (3) är olika poster för samma byte av 5: e graden.

Den kanoniska formen av substitution

I synnerhet kan varje substitution av den n: e graden A skrivas i kanonisk form

det vill säga med ett naturligt antal nummer i den översta raden. Med denna notation skiljer sig olika substitutioner från varandra genom permutationerna på bottenlinjen.

Ett exempel på nionde gradersubstitutionen är identitetssubstitutionen

där alla karaktärer förblir på plats.

Kommentar ... Det bör noteras att de övre och nedre raderna i posten (1) för substitution A spelar olika roller och genom att ordna om dem får vi generellt sett en annan substitution.

Loop Substitution Structure

Visa byte

(Dessutom alla siffror i 1 , i 2 , …, i m - annorlunda)

kallas en cykel med längd m.

För cykler införs en speciell beteckning:

Exempel 1.

Cykeln (2 3 4 1) fungerar enligt följande

Sats. Varje substitution kan sönderdelas i en produkt av oberoende cykler. Denna nedbrytning är unik upp till cykelns ordning.

Algoritm för att komponera en cykel:

1. Ta bytet, se vad det första elementet går till.

2.Vi skriver det resulterande elementet bakom det första elementet och hittar dess bild under substitutionsåtgärden.

3. Stäng cykeln så snart bilden sammanfaller med det element från vilket cykelns konstruktion började.

Exempel 2.

Expandera substitution

i produkten av oberoende cykler.

Lösning.

Sedan, då får vi cykeln (135). Kedjan 2 → 4 → 2 ger transpositionen (24). Även 6 → 8 → 6 ger transpositionen (68). 7 förblir på plats.

En en-till-en-mappning på sig själv (eller transformation) av en ändlig uppsättning N = (1, 2, 3, n) av de första n naturliga talen kallas en substitution av n-tal (eller en substitution med n-d-grad). Ersättningen skrivs vanligtvis i form av två strängar av siffror som är inneslutna inom parentes. Till exempel, en en-till-en-korrespondens av naturliga tal 1, 2 och 3, som ges av uppsättningen ((2, 3), (1, 2), (3, 1)) av ordnade par) skrivs som en substitution p av tredje graden (2 1 3 \ P = 13 2 1 J "där 2 går till 3, 1 - till 2 och 3 - till 1. Eftersom kartläggningen inte ändras när ordningen på de beställda paren är ändras kan samma substitution representeras i flera former: siffrorna i den översta raden är ordnade i en naturlig ordning. Sedan får ersättningen av den 71. graden formen (4.19) där t "i, t" 2, in är första n naturliga tal lokaliserade i en viss ordning. substitution och det totala antalet permutationer av den n: e graden sammanfaller med antalet n! permutationer för de första n elementen i uppsättningen N i bottenraden (4.19). Identisk ersättning av den n: e graden tar varje nummer i sig och kan skrivas i form (4.20) Sammansättning p2 ° Pi permutationer av n: e graden pi och P3 kallas nte effektbyte p = pipi) som är resultatet av sekventiell körning av kartläggningen, först ges av pi och sedan ges av /> 2. Sammansättningen av substitutionerna är skriven i form av deras produkt, men tas i omvänd ordning, och pip? frr \. Till exempel för substitutioner Det är tydligt att om p är en substitution av den n: e graden, så är det sv spelar rollen som ett neutralt element med avseende på kartläggningens sammansättningslag. Om raderna med substitutionen p i (4.19) byts ut, får vi den inversa substitutionen till substitutionen p och med den egenskap som är p "1 spelar rollen som ett element symmetriskt för p med avseende på sammansättningslagen för mappningar. Sålunda bildar uppsättningen P av n! -ersättningar av den n: e graden en multiplikationsgrupp (se tabell 4.1) med avseende på denna lag, som i det här fallet spelar rollen som en multiplikativ lag (Uppsättningen P kallas permutationsgruppen för n: e graden. Eftersom den första raden är oförändrad när den skrivs i formen (4.19) kan den n: e gradens permutation endast specificeras av den andra raden: Substitutionsgrupp n-talskompositionssymmetri-grupp av figuren m, dvs genom en permutation av de första n-elementen i uppsättningen N. Om i en sådan permutering utbyts två siffror (inte nödvändigtvis intill varandra), och resten är kvar i sin platser, då får vi en ny permutation. Denna transformation kallas permutationstransposition. Två siffror bildar en inversion i en permutation när den mindre av dem ligger till höger om den större (eller, som de säger, det större antalet i permutationen inträffar före den mindre). En permutation kallas även om det totala antalet inversioner i raden är jämnt och annorlunda udda. För att beräkna det totala antalet inversioner i viss omläggning av n-element, jämförs varje element sekventiellt, med början med det första till vänster, med alla som följer det, g bestämma antalet mindre nummer som står till höger. Detta ger antalet inversioner för ett visst element. N-1-siffrorna som erhållits på detta sätt läggs till. Exempel 4.12. men. Permutationen (1, 2, ..., n) är jämn för alla n, eftersom antalet inversioner i den är lika med noll. b. Permutation () innehåller 14 inversioner och är därför jämn. i. Permutation () innehåller 17 inversioner och är därför udda. Sats 4.7. Varje införlivande ändrar permutationens paritet. Låt oss först överväga fallet när de permuterade siffrorna r och j är sida vid sida, dvs. den ursprungliga permutationen och permutationen som erhållits genom införlivandet har formen där ellipser ersätter de siffror som inte påverkas av detta införlivande. I båda permutationerna utgör var och en av siffrorna t, j samma inversioner med de siffror som finns kvar på sina platser. Om siffrorna r och i den ursprungliga permutationen inte bildade inversioner kommer en ny inversion att visas efter införlivandet. Om dessa siffror i den ursprungliga permutationen bildade en inversion, försvinner den efter införlivandet, d.v.s. det totala antalet inversioner blir mindre. I båda fallen ändras permutationens paritet. Låt det nu finnas m-tal (m 6 N) mellan de permuterade siffrorna r och j, dvs. den ursprungliga permutationen har formen Ordningen på i och j kan bytas som ett resultat av en sekventiell förändring av platserna för angränsande nummer genom att utföra 2m + 1 steg (vi ordnar om t med klf och t, ​​som redan finns på platsen för A? I, c, etc. tills r in m-steg inte tar plats för kt och inte blir bredvid j; sedan byter vi i och Y, och slutligen kommer det att ta m fler steg för att successivt ordna om från kt-1, etc., varefter j kommer att äga rum i, och siffrorna k kt kommer att behålla sina platser). I detta fall ändras permutationens paritet ett udda antal (2m + 1) gånger. Därför har permutationerna (4.21) motsatta pariteter. Tänk på substitutionspost (4.19). Permutationerna som utgör dess övre och nedre linjer kan ha antingen samma eller motsatta pariteter. Övergången till vilken annan inspelning som helst kan utföras genom att sekventiellt utföra flera transpositioner i den övre raden och motsvarande transpositioner i den nedre raden. Men genom att göra en transponering i den översta raden (4.19) och en transponering av motsvarande element i den nedre raden ändrar vi samtidigt pariteten för båda permutationerna och bevarar därför sammanfallet eller motsatsen till deras pariteter. Därav följer att för varje substitution av pariteten i de övre och nedre raderna antingen sammanfaller eller är motsatta. Substitutionsgruppsubstitution av n siffror sammansättning symmetri grupp i en figur Definition 4.10. En substitution kallas även om permutationerna i båda raderna har samma paritet och udda om det motsatta. Det är uppenbart att identitetspermutationen (4.20) är jämn, och pariteten för permutationen i formen (4.19) sammanfaller med pariteten för permutationen i dess nedre rad. Ovanstående kan generaliseras i förhållande till en en-till-en-mappning på sig själv (transformation) av vilken som helst begränsad uppsättning E- (ni, 02, an) (inte nödvändigtvis numerisk) om dess element är numrerade med de första n naturliga tal. Exempel 4.13. Låt vara hörn i en liksidig triangel (fig. 4.5). ^ När en uppsättning P av n! = 3! = 6 substitutioner där "b" 2, "h är tre naturliga tal 1, 2, 3 ordnade i någon ordning, beskriver gruppen i Fig. 4,5 symmetrier av denna triangel, dvs. sådana förskjutningar av triangeln i planet där den sammanfaller med sig själv. Identitetsersättningen e, när, lämnar triangeln på plats. För (jämna utbyten a och 0) roterar triangeln moturs relativt punkt O respektive med vinklarna a = 3 (se figur 4.5). För (udda byte q) roterar triangeln runt symmetriaxeln OA. Rotationer runt symmetriaxlarna OB och OS ger udda substitutioner z respektive z för 4 = 3, "2 = 2," z = 1 och "1 = 2," 2 = 1, "Z = 3. Produktpip? någon av dessa substitutioner anger också en av triangeljusteringsoperationerna (till exempel qr = /?). I den vänstra kolumnen och den översta raden i tabellen. 4.2 notationen för substitutionerna p1 respektive p2 placeras respektive på de återstående platserna - produkterna pip? dessa utbyten. I varje rad och i varje kolumn i tabellen. 4.2 det finns en identisk ersättning e, d.v.s. varje operation är symmetrisk (eller invers), och för rotationsfunktionen kring vilken symmetriaxel som helst (och, naturligtvis, för den samma operationen) är själva denna operation den omvända. Tabellen är asymmetrisk med avseende på dess huvuddiagonal (passerar genom de övre vänstra och nedre högra elementen), vilket återigen visar att produkten av permutationer inte är kommutativ. Den betraktade uppsättningen P av permutationer kallas också figurens symmeturgrupp (i detta fall en liksidig triangel). På samma sätt kan du konstruera en symmetri-grupp av alla andra geometriska objekt som en uppsättning av alla transformationer i det metriska utrymmet som kombinerar det med sig själv (till exempel symmetri-gruppen i en kvadrat, kub, tetraeder osv.). Det är från dessa positioner som E.S. Fedorov konstruerade 1890 en klassificering av regelbundna rumsliga poängsystem som tillämpades på kristallografi. Det var historiskt den första tillämpningen av gruppteori direkt på naturvetenskap. Frågor och uppgifter 4.1. Kontrollera om kompositionslagen (operation) m har egenskaperna associativitet och kommutativitet på uppsättningen E: där GCD är den största gemensamma delaren av två naturliga tal. 4.2. Bestäm vilka algebraiska strukturer som bildas av följande numeriska uppsättningar med avseende på de angivna kompositionslagen: a) en av uppsättningarna med avseende på addition och med avseende på multiplikation; b) uppsättningen av alla jämna tal med avseende på addition och multiplikation; c) en uppsättning grader av ett givet verkligt antal af OO med heltalsexponenter med avseende på multiplikation; d) uppsättningen av alla komplexa rötter av en given grad n ∈ N från enhet med avseende på multiplikation; e) Uppsättningen av komplexa rötter i alla grader n € 14 från enhet med avseende på multiplikation. f) en uppsättning komplexa tal med en given modul r ∈ R med avseende på multiplikation; g) uppsättningen komplexa tal med modul som inte överstiger ett givet antal R Φ 0, med avseende på addition och med avseende på multiplikation; h) uppsättningen komplexa tal med icke-nollmodul placerad på strålarna som kommer från ursprunget och bildar vinklar y> 2i »¥> m med Ox-axeln med avseende på multiplikation. i) uppsättningen P (E) för alla delmängder av någon uppsättning E med avseende på funktionerna för symmetrisk skillnad och skärningspunkt och med avseende på var och en av dem separat. 4.3. På uppsättningen E = (o, 6, c) i en av tabellerna ges kompositionslagen m. För var och en av dessa lagar, bestäm dess egenskaper, ange ett neutralt element och par symmetriska element (om de finns), fastställa typen av algebraisk struktur. 4.4. Additiva (+) och multiplikativa (*) kompositionslagar ges på uppsättningen E = (o, 6, c) med hjälp av tabeller. För var och en av dessa lagar, bestäm dess egenskaper, ange det neutrala elementet och par symmetriska element (om de finns). Vilken algebraisk struktur bildar uppsättningen E med avseende på var och en av de givna lagarna och vad - med avseende på båda lagarna? Vilken mening får dessa lagar i den numeriska uppsättningen om vi lägger a = 1, 6 = 2, c = 3? 4.5. Additiva (+) och multiplikativa (*) kompositionslagar ges på uppsättningen E = (0, 1, ru q) med hjälp av tabeller. För var och en av dessa lagar, bestäm dess egenskaper, ange det neutrala elementet och par symmetriska element (om de finns). Vilken algebraisk struktur bildar uppsättningen E med avseende på var och en av de givna lagarna och vad - med avseende på båda lagarna? 4.6. Bevisa egenskaperna för operationer för addition och multiplicering av komplexa tal. 4.7. Hitta de verkliga och imaginära delarna av komplexa tal: 4.8. Bevisa likheterna: Permutationsgruppens permutation av n siffror sammansättning symmetri grupp av en figur 4.9. Bevisa att | £ C. Under vilka förhållanden blir dessa ojämlikheter lika? 4.10. Hitta alla komplexa tal konjugerade till dess a) kvadrat och b) kub. 4.11. Låt tre punkter zlf z3 ges på det komplexa planet. 1. Hitta punkten r, som bestämmer positionen för masscentrum för systemet med materialpunkter med massorna mi, m2) m3 vid de givna tre punkterna. Under vilket tillstånd kommer masscentrum att vara vid ursprunget? 2. De givna punkterna är triangelns hörn. Hitta skärningspunkten för dess medianer. Under vilket villkor kommer det att vara vid ursprunget? 3. De givna punkterna är de tre hörnpunkterna A \% А2у i parallellogrammet. Hitta dess fjärde toppunkt L4, Motsatt A2. Under vilket villkor kommer det att vara vid ursprunget? 4. Under vilket villkor ligger de angivna punkterna på en rak linje? 5. Hitta mitten av cirkeln som passerar genom de angivna punkterna. Under vilket villkor kommer det att vara vid ursprunget? 6. Hur lokaliseras de givna punkterna om | zi | = \ z2 \ = = 1 * s | φ 0 och zi + z2 + z3 = 0? 4.12. Hitta uppsättningen punkter i det komplexa planet, givet av villkoret: 4.13. Bevisa likheter: a 4.14. Är jämlikheten sann (* 4.15. Hitta produkten av alla rötter av grad n ∈ N av enhet. 4.16. Är siffran (2 + i) / (2- «) en rot till någon kraft av enhet? 4.17. Hitta komplexa nummer som motsvarar motsatta hörn av kvadraten om de andra två hörnpunkterna motsvarar siffrorna z \ och 23. 4.18 Hitta de komplexa siffrorna som motsvarar hörnen på en vanlig n-gon om siffrorna z \ och 22 motsvarar dess två angränsande hörn 4.19 Bevisa att polynomets heltal-nollor med heltalskoefficienter är delare av dess konstanta term (koefficient an) och hitta polynomernas hel-nollor: 4.20 Bevisa att varje polynom av udda grad med verkliga koefficienter har minst en reell noll. 4.21. Hitta polynom i minsta grad med verkliga koefficienter, vars nollor är: a) 3 och 2-i; b) t (root of multiplicity 2) och -1-i; c) 0, 1, i. 4.22. Hitta: a) ett polynom med nollor x \ förutsatt att siffrorna a? I, X2 och a? Z är nollor på polynom x3 -x2 -1; b) värdet av a, vid vilket nollställena för polynomet x3-1-x2 + 2a: + a bildar en geometrisk progression; c) summan av kvadrater och summan av kuber med nollor av polynom 8a: 4 - 5®2 + 2 «+ 1; d) summan av alla polynomens koefficienter: 1); e) Polynom P (x) i minsta grad efter villkoret: Hitta pariteten för substitutionerna: 4.24. Skriv ner gruppens symmetrigrupp, hitta pariteten för varje substitution från denna grupp, bygg en tabell som liknar tabellen. 4.2 och analysera den.