Substitution of degree n. Exponentiation: rules, examples. Exponentiation concept

Target: consider the concept of substitution, identical substitution,

explain how the operations of multiplying substitutions, finding inverse substitutions are performed,

list the properties of the product of substitutions,

consider the concepts of inversion, even-odd substitutions

show how substitutions are applied in cryptography

Once Thomas received a telegram from one of his friends. This telegram was strange. This is what was written in it: "yazhzeirponchors medzh".

Can you "read" this text? Thomas, after a little thought, understood the secret of this telegram. He was invited to visit. He decided to answer in the same spirit. I composed a reply telegram and encrypted it in the same way. The result is a record of two lines:

"I'll come meet you on Saturday",

"" etyachertswutobbuswudeirp "".

After the end of the encryption, Thomas wanted to conduct all his correspondence with a friend only in encrypted texts, changing from time to time the method of encryption. Therefore, he zealously set about developing an encryption method.

He decided to replace the letters of the original text with the position numbers that these letters occupy. Here is the list of numbers Foma received for his friend's telegram:

(1, 2, 3, ... , 18).

Then he noticed that the cipher text differs from the original only in the changed order of the beeches. How the letter order changes is easy to see with the same position numbers. For example, the cipher text of a telegram from a friend Thomas could now be presented in the form of a list:

(18, 17, 16, . . . , 3, 2, 1).

Comparing these two lists gives a clue to encrypting the text:

.

The symbolic record reads like this: "1 goes to 18". Another notation is often used instead:.

The direction of the arrows determines the order encryption text. For example, a letter in the first position in the cipher text should occupy the 18th position in the cipher text.

If the direction of the arrows is changed to the opposite, then the same two-line table will determine the order transcripts text. For example, a letter in the 18th position in the ciphertext should occupy the first position in the decrypted text.

Finally, if the first line is always associated with the source text, then there is no need to use arrows. (When encrypted, the original text is the encrypted text, and when decrypted, it is encrypted).

Realizing all this, Thomas quickly wrote down the key to the second encryption of his telegram:

It remains only to communicate this key to your friend in some way, and the secrecy of the correspondence is guaranteed!

If you understand Thomas's ideas, then here is his encrypted favorite saying:

"water boil".

It is encrypted with the key:

Encryption key:

"Trust but check!"

You probably already guessed that there are a lot of encryption keys of this kind. Each of them can be represented as a two-line table:

.

Here, the top line contains all natural numbers from 1 to NS in ascending order. The bottom line is obtained by some permutation of numbers from the top line. The whole table as a whole is called order substitution NS.

Consider the set , where, each element in which is presented only once. Then a one-to-one mapping of a set onto itself is called substitution degree NS.

Lots of substitutions NS-th degree is indicated.

The relation is binary, therefore, substitutions are usually written in the form of a two-row matrix, in the first row of which the preimages are written, and in the second - their images:

If the preimages (arguments) are arranged in ascending order (then a substitution record of this kind is called canonical... If the arguments are not written in ascending order, then by rearranging the columns (in this case the substitution itself does not change, but only the pronunciation order of the matches changes), you can bring the top row to an ordered form:

Whenever possible, we will use the canonical notation. Such a recording was encountered when we recorded a permutation from NS elements. Note that the preimage of the permutation is an arbitrary finite set, and the preimage of the permutation is obligatory.

Let us find the number of possible different substitutions of the degree NS... Since each canonical permutation is equivalent to the corresponding permutation, the number of permutations NS-th degree is equal to the number of permutations from NS elements, that is, the set consists of elements.

Let's go back to Thomas. Using Key Substitution

he encrypted a one-word message and sent it to a friend. He encrypted the unencrypted message again, but with a different key.

The resulting double-encrypted message he addressed to you: "snoas".

Decrypt this message. , " Pine»

You can make the decryption process much faster if you know how one algebraic operation is performed on substitutions. This operation is called multiplication of substitutions.(If you want, you can call it differently, because it has nothing to do with the usual multiplication of numbers).

Let's look at an example of how it is performed. Let's multiply the substitutions with which Foma's message was encrypted:

The multiplication procedure is reduced to sequential substitutions.

In the first substitution ( BUT): 1 → 5;

in the second substitution (IN): 5 → 1;

As a result, we get: 1 → 1.

Similarly, from "2 → 2" and "2 → 3" it follows: "2 → 3". Carrying out three more arguments of this type, we obtain the product substitution

Using the substitution AB as a scrambler, you can now decrypt Thomas "snoas" message in one go. At the same time, you will control yourself. ( VA= « pump»)

If you are interested, you can come up with your own message scramblers and keep secret correspondence with friends.

Deciphering messages, you became familiar with the algebraic operation on new substitution objects. If some of you are interested not only in encryption, but also in substitutions themselves, then you can get to know them better by completing the following tasks.

EXERCISE 1... Find the products of the substitutions:

TASK 2. Find a piece VA substitutions BUT and IN, discussed above. Using the substitution VA as a scrambler, decipher the message "cod" again. Compare the result with the result of the previous decryption. Then you can tell whether the permutation multiplication is commutative.

Let there be given two substitutions and, moreover

We figured out what the degree of a number is in general. Now we need to understand how to correctly calculate it, i.e. raise numbers to a power. In this material, we will analyze the basic rules for calculating the degree in the case of a whole, natural, fractional, rational and irrational exponent. All definitions will be illustrated with examples.

Exponentiation concept

Let's start by formulating basic definitions.

Definition 1

Exponentiation- this is the calculation of the value of the power of a number.

That is, the words "calculating the value of a power" and "raising to a power" mean the same thing. So, if the problem is "Raise the number 0, 5 to the fifth power", it should be understood as "calculate the value of the power (0, 5) 5.

Now we will give the basic rules that must be adhered to in such calculations.

Let's remember what the degree of a number with a natural exponent is. For a power with base a and exponent n, this will be the product of n -th number of factors, each of which is equal to a. It can be written like this:

To calculate the value of the power, you need to perform the action of multiplication, that is, multiply the bases of the power a specified number of times. The very concept of a degree with a natural indicator is based on the ability to quickly multiply. Here are some examples.

Example 1

Condition: raise - 2 to the power of 4.

Solution

Using the definition above, we write: (- 2) 4 = (- 2) · (- 2) · (- 2) · (- 2). Next, we just need to follow the specified steps and get 16.

Let's take a more complicated example.

Example 2

Calculate the value 3 2 7 2

Solution

This record can be rewritten as 3 2 7 · 3 2 7. Earlier, we looked at how to correctly multiply the mixed numbers mentioned in the condition.

Let's perform these actions and get the answer: 3 2 7 3 2 7 = 23 7 23 7 = 529 49 = 10 39 49

If the problem indicates the need to raise irrational numbers to a natural power, we need to first round their bases to a digit that will allow us to get an answer of the required accuracy. Let's look at an example.

Example 3

Square π.

Solution

First, let's round it to the nearest hundredth. Then π 2 ≈ (3, 14) 2 = 9, 8596. If π ≈ 3. 14159, then we get a more accurate result: π 2 ≈ (3, 14159) 2 = 9, 8695877281.

Note that the need to calculate the degrees of irrational numbers in practice arises relatively rarely. We can then write the answer in the form of the power itself (ln 6) 3 or transform, if possible: 5 7 = 125 5.

Separately, it should be indicated what the first degree of a number is. Here you can simply remember that any number raised to the first power will remain itself:

This is clear from the entry. .

It does not depend on the base of the degree.

Example 4

So, (- 9) 1 = - 9, and 7 3, raised to the first power, will remain equal to 7 3.

For convenience, we will analyze separately three cases: if the exponent is a positive integer, if it is zero, and if it is a negative integer.

In the first case, this is the same as raising to a natural power: after all, positive integers belong to the set of natural numbers. We have already described how to work with such degrees above.

Now let's see how to correctly raise to the zero power. With a radix other than zero, this calculation always outputs 1. We have already explained earlier that the 0th power of a can be defined for any real number not equal to 0, and a 0 = 1.

Example 5

5 0 = 1 , (- 2 , 56) 0 = 1 2 3 0 = 1

0 0 - not defined.

We are left with only a case of a degree with a whole negative exponent. We have already discussed that such degrees can be written as a fraction 1 a z, where a is any number, and z is an integer negative exponent. We see that the denominator of this fraction is nothing more than an ordinary power with a whole positive exponent, and we have already learned how to calculate it. Let's give examples of tasks.

Example 6

Raise 2 to the power - 3.

Solution

Using the definition above, we write: 2 - 3 = 1 2 3

Let's calculate the denominator of this fraction and get 8: 2 3 = 2 · 2 · 2 = 8.

Then the answer is: 2 - 3 = 1 2 3 = 1 8

Example 7

Raise 1, 43 to the power - 2.

Solution

Let's reformulate: 1, 43 - 2 = 1 (1, 43) 2

We calculate the square in the denominator: 1.43 · 1.43. Decimal fractions can be multiplied in this way: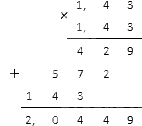

As a result, we got (1, 43) - 2 = 1 (1, 43) 2 = 1 2, 0449. It remains for us to write this result in the form of an ordinary fraction, for which it is necessary to multiply it by 10 thousand (see the material on the conversion of fractions).

Answer: (1, 43) - 2 = 10000 20449

A separate case is raising a number to the minus first power. The value of this degree is equal to the inverse of the original base value: a - 1 = 1 a 1 = 1 a.

Example 8

Example: 3 - 1 = 1/3

9 13 - 1 = 13 9 6 4 - 1 = 1 6 4 .

How to raise a number to a fractional power

To perform such an operation, we need to recall the basic definition of a degree with a fractional exponent: a m n = a m n for any positive a, integer m and natural n.

Definition 2

Thus, the calculation of the fractional power must be performed in two steps: raising to an integer power and finding the root of the nth power.

We have the equality a m n = a m n, which, given the properties of the roots, is usually used to solve problems in the form a m n = a n m. This means that if we raise the number a to a fractional power of m / n, then first we extract the nth root of a, then we raise the result to a power with an integer exponent m.

Let us illustrate with an example.

Example 9

Calculate 8 - 2 3.

Solution

Method 1. According to the basic definition, we can represent it as: 8 - 2 3 = 8 - 2 3

Now let's calculate the degree under the root and extract the third root from the result: 8 - 2 3 = 1 64 3 = 1 3 3 64 3 = 1 3 3 4 3 3 = 1 4

Method 2. We transform the basic equality: 8 - 2 3 = 8 - 2 3 = 8 3 - 2

After that, extract the root 8 3 - 2 = 2 3 3 - 2 = 2 - 2 and square the result: 2 - 2 = 1 2 2 = 1 4

We see that the solutions are identical. You can use it in any way you like.

There are times when the degree has an exponent expressed as a mixed number or decimal fraction. For ease of calculations, it is better to replace it with an ordinary fraction and count it as indicated above.

Example 10

Raise 44.89 to the power of 2.5.

Solution

We convert the value of the indicator into an ordinary fraction: 44, 89 2, 5 = 44, 89 5 2.

And now we perform in order all the actions mentioned above: 44, 89 5 2 = 44, 89 5 = 44, 89 5 = 4489 100 5 = 4489 100 5 = 67 2 10 2 5 = 67 10 5 = = 1350 125 107 100 000 = 13 501, 25107

Answer: 13 501, 25107.

If there are large numbers in the numerator and denominator of a fractional exponent, then calculating such degrees with rational exponents is a rather difficult job. It usually requires computing.

Let us dwell separately on the degree with a zero base and a fractional exponent. An expression of the form 0 m n can be given the following meaning: if m n> 0, then 0 m n = 0 m n = 0; if m n< 0 нуль остается не определен. Таким образом, возведение нуля в дробную положительную степень приводит к нулю: 0 7 12 = 0 , 0 3 2 5 = 0 , 0 0 , 024 = 0 , а в целую отрицательную - значения не имеет: 0 - 4 3 .

How to raise a number to an irrational power

The need to calculate the value of the degree, in the exponent of which there is an irrational number, does not arise so often. In practice, the task is usually limited to calculating an approximate value (up to a certain number of decimal places). This is usually calculated on a computer due to the complexity of such calculations, so we will not dwell on this in detail, we will indicate only the main provisions.

If we need to calculate the value of the exponent a with an irrational exponent a, then we take the decimal approximation of the exponent and calculate it. The result will be an approximate answer. The more accurate the decimal approximation, the more accurate the answer. Let's show with an example:

Example 11

Calculate the approximate value of 2 to the 1.174367 power ....

Solution

We will restrict ourselves to the decimal approximation a n = 1, 17. Let's make calculations using this number: 2 1, 17 ≈ 2, 250116. If we take, for example, the approximation a n = 1, 1743, then the answer will be a little more accurate: 2 1, 174367. ... ... ≈ 2 1, 1743 ≈ 2, 256833.

If you notice an error in the text, please select it and press Ctrl + Enter

Definition 5. Substitution Nth degree is called a one-to-one mapping of the Set onto itself. Substitution is usually written using two N-permutations written one below the other:

, (1)

Where through denotes the number into which, when substituted, the element goes i, i.e.; i = 1,2, ..., N.

In a lookup record, you can swap columns in any way. For example, all three of the following substitutions are equal.

. (2)

In particular, any substitution N-th degree can be written as:

.

With this form of notation, various substitutions differ only by the permutations in the bottom line. Then, by virtue of Theorem 1, we obtained the following statement.

Theorem 4.The number of different substitutions of the nth degree is N.

Definition 6.By the number of inversions in the substitution is the sum of the number of inversions in the first and second substitution lines.

We denote the number of inversions in the substitution by the symbol. The substitution is called Even, if the number is even, and it is called Odd if the number is odd. A wildcard is a number:

.

Therefore, the wildcard is 1 or -1, depending on whether the substitution is even or odd.

By virtue of Theorem 2, when the columns in the substitution are permuted, the parities of the permutations in the lower and upper rows of the substitution are simultaneously reversed. Consequently, the parity of the permutation is preserved. From this and Theorem 3 we obtain the following properties of substitutions.

1. Parity and wildcard are independent of the form of the wildcard.

2. When N> 1 number of even substitutions N-th degree is equal to the number of odd substitutions and is equal to.

Example 4. Substitution (2) is odd and has a -1 sign, although for different notation forms it has 3, 7, 5 inversions.

Let us show that the set of all permutations N-th degree forms a group with respect to the operation of multiplication of substitutions, defined below. This group is of great importance in algebra, called Symmetric Group and is indicated by the symbol.

Definition 7. By the product of substitutions and N-th degree is the composition of These statements as mappings, that is, for any we have. We denote

Since the composition of two bijective mappings is a bijective mapping, then the product of two permutations N-th degree there are coasters N-th degree. In practical multiplication of substitutions, the right substitution is performed first and then the left one. For example,

Theorem 5.The set of all permutations of the nth degree forms a group with respect to the operation of multiplication of permutations.

Proof. In view of the above, the operation of multiplication of substitutions is a binary algebraic operation. Let us check the axioms of the group.

Substitution multiplication is associative. Indeed, let it be. Then for any

Definition ... Any one-to-one mapping of the set A of the first n natural numbers onto itself is called substitutionn-th degree, and, obviously, any permutation A can be written using two permutations signed one under the other

Through α i here denotes the number into which the substitution A transforms the number i , i = 1, 2, …, n.

Let's write one under the other two permutations of n characters, taking the resulting two lines in parentheses; for example n = 5:

We will say that the number is 3 goes over into number 5, number 5 goes into 2, number 1 goes into 3, number 4 goes into 4 (or remains in place), and finally, number 2 goes into 1. Thus, two permutations, written under each other in the form (2) define some one-to-one mapping sets of the first five natural numbers onto itself, that is, a mapping that assigns to each of the natural numbers 1, 2, 3, 4, 5 one of the same natural numbers, and different numbers are assigned different numbers.

It is clear that the one-to-one mapping of the set of the first five natural numbers that we obtained with the help of (2) could be obtained by writing one under the other and some other pairs of permutations of five symbols. These records are obtained from (2) by several transpositions (permutations) of columns; such are, for example,

In all of these entries, 3 goes into 5, 5 into 2, and so on.

Substitution A has many different entries of the form (1). So, (2) and (3) are different records of the same substitution of the 5th degree.

The canonical form of substitution

In particular, any substitution of the nth degree A can be written in the canonical form

that is, with a natural arrangement of numbers in the top line. With this notation, various substitutions differ from each other by the permutations on the bottom line.

An example of the nth degree substitution is the identity substitution

in which all characters remain in place.

Comment ... It should be noted that the upper and lower lines in the entry (1) of the substitution A play different roles and, by rearranging them, we, generally speaking, get a different substitution.

Loop Substitution Structure

View substitution

(Moreover, all numbers i 1 , i 2 , …, i m - different)

is called a cycle of length m.

For cycles, a special designation is introduced:

Example 1.

The cycle (2 3 4 1) operates as follows

Theorem. Each substitution can be decomposed into a product of independent cycles. This decomposition is unique up to the order of cycles.

Algorithm for composing a cycle:

1. Take the substitution, see what the first element goes to.

2.We write the resulting element behind the first element and find its image under the substitution action.

3. As soon as the image coincides with the element from which the construction of the cycle began, close the cycle.

Example 2.

Expand substitution

into the product of independent cycles.

Solution.

Since, then we get the cycle (135). The chain 2 → 4 → 2 gives the transposition (24). Also 6 → 8 → 6 gives the transposition (68). 7 remains in place.

A one-to-one mapping onto itself (or transformation) of a finite set N = (1, 2, 3, n) of the first n natural numbers is called a substitution of n numbers (or a substitution of n-d degree). The substitution is usually written in the form of two strings of numbers enclosed in parentheses. For example, a one-to-one correspondence of natural numbers 1, 2 and 3, given by the set ((2, 3), (1, 2), (3, 1)) of ordered pairs) is written as a substitution p of the third degree (2 1 3 \ P = 13 2 1 J "in which 2 goes to 3, 1 - to 2, and 3 - to 1. Since the mapping does not change when the order of the ordered pairs is changed, the same substitution can be represented in several forms: the numbers in the top line are arranged in a natural order. Then the substitution of the 71st degree takes the form (4.19) where t "i, t" 2, in are the first n natural numbers located in a certain order. substitution, and the total number of permutations of the nth degree coincides with the number of n! permutations of the first n elements of the set N in the bottom line (4.19). Identical substitution of the nth degree takes each number into itself and can be written in the form (4.20) Composition p2 ° Pi permutations of the nth degree pi and P3 are called substitution of the nth degree p = pipi) which is the result of sequential execution of the mapping, first given by pi, and then given by /> 2. The composition of the substitutions is written in the form of their product, but taken in reverse order, and pip? frr \. For example, for substitutions It is clear that if p is a substitution of the nth degree, then that is, en plays the role of a neutral element with respect to the composition law of mappings. If the rows of the substitution p in (4.19) are interchanged, then we obtain the inverse substitution to the substitution p and having the property that is p "1 plays the role of an element symmetric for p with respect to the composition law of mappings. Thus, the set P of n! substitutions of the nth degree forms a multiplicative group (see Table 4.1) with respect to this law, which in this case plays the role of a multiplicative law ( The set P is called the nth degree permutation group.Since the first row is unchanged when written in the form (4.19), the nth degree substitution can be specified only by the second row: Substitution group n number composition symmetry group of the figure m that is, by a permutation of the first n elements of the set N. If in such a permutation any two numbers are interchanged (not necessarily adjacent), and the rest are left in their places, then we get a new permutation. This transformation is called the permutation transposition. Two numbers form an inversion in a permutation when the smaller of them is located to the right of the larger (or, as they say, the larger number in the permutation occurs before the smaller one). A permutation is called even if the total number of inversions in its row is even, and odd otherwise. To calculate the total number of inversions in some rearrangement of n elements, each element is sequentially compared, starting with the first on the left, with all following it, g determine the number of smaller numbers standing to the right. This gives the number of inversions of a given element. The n-1 numbers obtained in this way are added. Example 4.12. but. The permutation (1, 2, ..., n) is even for any n, since the number of inversions in it is equal to zero. b. Permutation () contains 14 inversions and is therefore even. in. Permutation () contains 17 inversions and is therefore odd. Theorem 4.7. Any transposition changes the parity of the permutation. Let us first consider the case when the permuted numbers r and j are side by side, i.e. the original permutation and the permutation obtained by the transposition have the form where ellipses replace those numbers that are not affected by this transposition. In both permutations, each of the numbers t, j constitutes the same inversions with the numbers that remain in their places. If the numbers r and in the original permutation did not form inversions, then after the transposition one new inversion will arise. If these numbers in the original permutation formed an inversion, then after the transposition it will disappear, i.e. the total number of inversions becomes one less. In both cases, the parity of the permutation changes. Now let there be m numbers (m 6 N) between the permuted numbers r and j, i.e. the original permutation is of the form The order of i and j can be swapped as a result of a sequential change of places of neighboring numbers by performing 2m + 1 steps (we rearrange t with klf then t, which is already in place of A? i, c, etc., until r in m steps does not take the place of kt and does not become next to j; then we swap i and Y, and, finally, it will take m more steps to successively rearrange j from kt-1, etc., after which j will take place i, and the numbers k kt will retain their places). In this case, the parity of the permutation changes an odd number (2m + 1) times. Therefore, the permutations (4.21) have opposite parities. Consider the notation of the substitution (4.19). The permutations that make up its top and bottom lines can have either the same or opposite parities. The transition to any other recording can be carried out by sequentially performing several transpositions in the upper line and the corresponding transpositions in the lower line. However, making one transposition in the top row (4.19) and one transposition of the corresponding elements in the bottom row, we simultaneously change the parities of both permutations and therefore preserve the coincidence or opposite of their parities. Hence it follows that for any substitution of the parity of the upper and lower lines either coincide or are opposite. Substitution group substitution of n numbers composition symmetry group of a figure Definition 4.10. A substitution is called even if the permutations in both rows have the same parity, and odd if the opposite. It is clear that the identity permutation (4.20) is even, and the parity of the permutation given in the form (4.19) coincides with the parity of the permutation in its bottom row. The above can be generalized in relation to a one-to-one mapping onto itself (transformation) of any finite set E- (ni, 02, an) (not necessarily numeric) if its elements are numbered with the first n natural numbers. Example 4.13. Let be the vertices of an equilateral triangle (Fig. 4.5). ^ When a set P of n! = 3! = 6 substitutions where "b" 2, "s are three natural numbers 1, 2, 3 arranged in some order, describes the group in Fig. 4.5 symmetries of this triangle, i.e. such displacements of the triangle in the plane, at which it coincides with itself. The identity substitution e, when, leaves the triangle in place. For (even substitutions a and 0), the triangle rotates counterclockwise relative to the point O, respectively, by angles a = 3 (see Fig. 4.5). For (odd substitution q), the triangle rotates around the axis of symmetry OA. Rotations around the symmetry axes OB and OS give odd substitutions z and z, respectively, for 4 = 3, "2 = 2," z = 1 and "1 = 2," 2 = 1, "Z = 3. Product pip? any of these substitutions also specifies one of the triangle alignment operations (for example, qr = /?). In the left column and the top row of the table. 4.2 the notation for the substitutions p1 and p2 are placed, respectively, and in the remaining places - the products pip? these substitutions. In each row and in each column of the table. 4.2 there is an identical substitution e, i.e. every operation has a symmetric (or inverse), and for the operation of rotation with respect to any axis of symmetry (and, of course, for the identical operation), this operation itself is inverse. The table is asymmetric with respect to its main diagonal (passing through the top-left and bottom-right elements), which once again shows that the product of permutations is non-commutative. The considered set P of permutations is also called the symmetry group of the figure (in this case, an equilateral triangle). Similarly, you can construct a symmetry group of any other geometric object as a set of all transformations of the metric space that combine it with itself (for example, the symmetry group of a square, cube, tetrahedron, etc.). It is from these positions that E.S. Fedorov in 1890 constructed a classification of regular spatial systems of points as applied to crystallography. It was historically the first application of group theory directly to natural science. Questions and tasks 4.1. Check whether the composition law (operation) m has the properties of associativity and commutativity on the set E: where GCD is the greatest common divisor of two natural numbers. 4.2. Establish which algebraic structures are formed by the following numerical sets with respect to the indicated composition laws: a) one of the sets with respect to addition and with respect to multiplication; b) the set of all even numbers with respect to addition and multiplication; c) a set of degrees of a given real number af OO with integer exponents relative to multiplication; d) the set of all complex roots of a given degree n ∈ N from unity with respect to multiplication; e) the set of complex roots of all degrees n € 14 from unity with respect to multiplication; f) a set of complex numbers with a given modulus r ∈ R with respect to multiplication; g) the set of complex numbers with modulus not exceeding a given number R Φ 0, with respect to addition and with respect to multiplication; h) the set of complex numbers with nonzero modulus located on the rays emerging from the origin and forming angles with the Ox axis y> 2i »¥> m with respect to multiplication. i) the set P (E) of all subsets of some set E with respect to the operations of symmetric difference and intersection and with respect to each of them separately. 4.3. On the set E = (o, 6, c) of one of the tables, the composition law m is given. For each of these laws, determine its properties, indicate a neutral element and pairs of symmetric elements (if they exist), establish the type of algebraic structure. 4.4. Additive (+) and multiplicative (*) composition laws are given on the set E = (o, 6, c) with the help of tables. For each of these laws, determine its properties, indicate the neutral element and pairs of symmetric elements (if they exist). What algebraic structure does the set E form with respect to each of the given laws and what - with respect to both laws? What meaning do these laws acquire in the numerical set if we put a = 1, 6 = 2, c = 3? 4.5. Additive (+) and multiplicative (*) laws of composition are given on the set E = (0, 1, ru q) with the help of tables. For each of these laws, determine its properties, indicate the neutral element and pairs of symmetric elements (if they exist). What algebraic structure does the set E form with respect to each of the given laws and what - with respect to both laws? 4.6. Prove the properties of operations of addition and multiplication of complex numbers. 4.7. Find the real and imaginary parts of complex numbers: 4.8. Prove the equalities: Permutation group permutation of n numbers composition symmetry group of a figure 4.9. Prove that | £ C. Under what conditions do these inequalities become equalities? 4.10. Find all complex numbers conjugate to its a) square and b) cube. 4.11. Let three points zlf z3 be given on the complex plane. 1. Find the point r, which determines the position of the center of mass of the system of material points with masses mi, m2) m3 located at the given three points. Under what condition will the center of mass be at the origin? 2. The given points are the vertices of the triangle. Find the point of intersection of its medians. Under what condition will it be at the origin? 3. The given points are the three vertices А \% А2у of the parallelogram. Find its fourth vertex L4, Opposite A2. Under what condition will it be at the origin? 4. Under what condition do the given points lie on one straight line? 5. Find the center of the circle passing through the given points. Under what condition will it be at the origin? 6. How are the given points located if | zi | = \ z2 \ = = 1 * s | φ 0 and zi + z2 + z3 = 0? 4.12. Find the set of points of the complex plane given by the condition: 4.13. Prove the equalities: a 4.14. Is the equality true (* 4.15. Find the product of all roots of degree n ∈ N of unity. 4.16. Is the number (2 + i) / (2- «) a root of some power of unity? 4.17. Find the complex numbers corresponding to the opposite vertices of the square if the other two vertices correspond to the numbers z \ and 23. 4.18 Find the complex numbers corresponding to the vertices of a regular n-gon if the numbers z \ and 22 correspond to its two neighboring vertices 4.19 Prove that the integer zeros of the polynomial with integer coefficients are divisors of its constant term (coefficient an), and find the integer zeros of the polynomials: 4.20 Prove that every polynomial of odd degree with real coefficients has at least one real zero. 4.21. Find the polynomial of the smallest degree with real coefficients, the zeros of which are: a) 3 and 2-i; b) t (root of multiplicity 2) and -1-i; c) 0, 1, i. 4.22. Find: a) a polynomial with zeros x \ provided that the numbers a? I, X2 and a? Z are zeros of the polynomial x3 -x2 -1; b) the value of a, at which the zeros of the polynomial x3-1-x2 + 2a: + a form a geometric progression; c) the sum of squares and the sum of cubes of zeros of the polynomial 8a: 4 - 5®2 + 2 «+ 1; d) the sum of all the coefficients of the polynomial: 1); e) the polynomial P (x) of the least degree by the condition: Find the parity of the substitutions: 4.24. Write down the group of symmetries of the square, find the parity of each substitution from this group, build a table similar to Table. 4.2, and analyze it.